例谈“什么是数学思维?”
姜彩清
我发在公众号里的《数学学习:要让孩子能学、会学与乐学》这篇文章,截止今天晚上10点,阅读量已达7597次了,我内心觉得挺有成就感的。不过,老婆却告诉我,她办公室的几个同事观点是,这篇文章的前半部分很精彩,通过“高水平”的一番闲扯,把育人的道理说得非常清楚明白,而后半部分涉及数学知识的教学,显得晦涩难懂——所以办公室里的这几个老师关注我的公众号,他们每次只读我文章的前半部分。
当然,老婆办公室的同事都是语文老师,她们对数学题不感兴趣也是可以理解的。不过,她们的说法还是给了我两点启发:一是要继续言简意赅的“扯”好修心养性或教书育人的真心感悟;二是如果无法避免数学方面的例子,就举一些简单的数学题目,方便家长朋友们,以及关注我公众号的一些语文老师,都能看懂,这样的文章才算完美一些(今天数学题例不多,且都是中低年级的内容)。

第一部分,简述两点感悟
感悟1:怎样才能拥有好心情?
人生在世,一是要知足常乐,二是不争强好胜——如此便会有好心情。
前者“知足常乐”就不赘述了,大家都懂的。针对后者“不争强好胜”想来多说几句。我们凡事都要懂得——不与人争,这是一种豁达自信的表现。
正如一位学者所言:“你若为大树,就不必跟小草争;你若为雄鹰,就不必跟小鸟争。”——的确,若我们真为强者,就应该与世人无争,无论对方是人是鬼,是“真善美”还是“假恶丑”。当你懂得不争的时候,其实你就处于人生的顶峰了。这时,静下心来,冷眼看世界,你就会有许多发现与收获。当我们什么都想明白了,也就没有什么放不下了。
经历过人生风雨,进入中老年后,我们就会明白,我们舍不得且心心念念的朋友,其实常常并没有舍不得我们,所以别高估自己在他人心目中的分量。换言之,我们与他人相处时,别期望什么,别希望什么,别盼望什么,更别指望得到什么,那么,我们就永远不会有失望、失落、懊恼与痛苦……
一言以蔽之,好心情真的是太重要了——每个人值得拥有,永远,永远!

感悟2:怎样更好地自我成长?
有人说,人的一生中有三次改变命运的机会,分别是学历,婚姻,自我觉醒。——我个人也是非常赞同这个观点的。
小时候家里穷,每到春种、秋收的时节,放学回家第一件事不是写作业,而是要去田地里帮着父母做农活。不得不说,农民真辛苦,风吹日晒,一年到头也挣不到几个钱。那时,我虽然年龄很小,但满脑子就是想“鲤鱼跳龙门”。于是乎,我便拼命地读书学习。初三毕业那一年,我顺利地考上了江苏省海州师范学校,成为我们村里当时第一个“中举”之人,从而摆脱了黑土地的束缚,走上了更广大的人生舞台。可以说,这辈子第一次改变自己命运的机会,被我紧紧地抓住了……
——因此,读书真的能改变自己的命运。
关于婚姻,有人这样说过——“真正的爱情,一定是双向奔赴的,它一定是一个人想垫脚,一个人想弯腰。”也就是双方同频共振,步调一致,琴瑟和鸣,恩爱有加。需要说明的是,白富美嫁给了穷小子,不一定就是一地鸡毛;而穷家女嫁给了高富帅,也不一定就是锦衣玉食。
我个人观点,最好还是讲究“门当户对”(即经济,学识,特别是人品,都要“门当户对”)。这样,双方生活在同一阶层,思想属于同一水平,往往更容易平等地沟通与交流,生活也更舒心与幸福。
但如果说,我们没有遇到对的人(能让我们越来越好的人),从而让我们的生活过得越来越差,那么,我们就要重新评估这份感情,是否还有存在的价值,必要时要学会及时止损,给自己松绑,绝不与烂人烂事纠缠一辈子。
——可见,步入婚姻是人性的第二次重生,真的非常重要。这是人改变命运的第二次机会。
人的一生,什么事都有可能发生,什么人都有可能遇到。当你发现生活中的不如意,并能想办法去克服或改变目前的窘境,那么恭喜你——你已经“自我觉醒”或是已经走在“自我觉醒”的路上了。“自我觉醒”的最直接表现是,不向多舛的命运低头,尝试用自己的智慧去应对,力求实现良好的改变。
韩愈说:“业精于勤而荒于嬉,行成于思而毁于随。”努力工作而得到酬劳是最现实的生活资本,勤奋拼搏而获得财富也是我们最现实的幸福源泉。这里,我们要强调,自我觉醒的意识出现,什么时候都不晚。种植一棵树的最好时间是十年前,其次就是现在(立即行动起来),不可拖延。
——不容质疑,自我觉醒与不断努力,是改变命运的最坚实的一张王牌。

第二部分,什么是数学思维
数学思维,顾名思义,就是运用数学的知识和方法来分析和解决问题的思维方式。它不仅仅是数学学科本身的核心素养,也是跨学科能力的重要体现。
它主要包括这样几个方面:一是逻辑推理能力(包括演绎推理和归纳推理。演绎推理是从普遍的原理出发,推导出特定的结论,而归纳推理则是从特定的观察和事实出发,归纳出普遍的规律);二是抽象思维能力(能够从具体的事物中抽象出数学概念和规律);三是空间想象能力(能够在大脑中形成空间物体的形象,进行空间位置的判断和操作);四是运算能力(包括基本的算术运算、代数运算等,良好的运算能力有助于数学思维的敏捷性和准确性);五是问题解决能力(能够面对问题,通过分析、假设、推理等方法,找到解决问题的策略和途径);六是数学建模能力(能够帮助我们把实际问题转化为数学问题,通过对数学模型来的分析,从而快速地解决一些复杂的问题);七是批判性思维能力(学会质疑和验证,批判性地思考问题)。
这样语言描述,可能大家不一定明白。下面,我来举例说明一下。

例1:从3、5、8这三张数字卡片中,每次选两张组成一个两位数,一共可以组成多少个不同的两位数?
这个简单吧,但要有序思维与有条理地表达,比如,按从小到大的顺序,依次为35,38,53,58,83,85,一共6个不同的两位数。
如果我把上面的题目修改一下,变成:“从3、5、6这三张数字卡片中,每次选两张组成一个两位数,一共可以组成多少个不同的两位数?”
此时,如果你认为与上面的题目毫无差别,还是组成6个不同的两位数,那么就错了——数学思维的缜密性告诉我们,这里是数字卡片,所以要考虑卡片上的数字6旋转180度后是9,所以后一题的答案是35,36,39,53,56,59,63,65,93,95,一共组成10个不同的两位数。
现在,大家对数学思维是不是有一点不同的认识了?
例2:甲、乙、丙三人各有连环画若干本,如果甲给乙5本,乙给丙10本,丙再给甲15本,那么三个人连环画都是35本。求甲、乙、丙三人原来各有多少本?
这道题的数量关系有点“绕人”,许多同学一筹莫展,无法下手解答。其实,我们只需要将题目中数量的变化过程,采用符号化的方法,把甲、乙、丙三人的变化情况理一理,转化成“填空题”的形式,就非常简单了(如下左图所示)。这样再倒推回去,就非常方便列出算式了(如下右图)。

例3:一个正方形(如下图)去掉一个小长方形,这时剩下的面积是70平方厘米。求原来正方形的面积是多少?
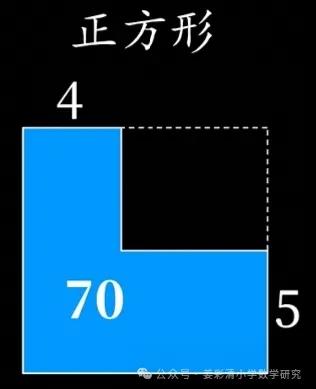
语文老师会说:“这是什么鬼东西?不好搞,我不搞了。”
初中数学老师会这样想:设个两个未知数X与Y,列出方程组,可以求解得出答案。

但小学生并不会这样思考,这种“复杂”的方程组,也超出了小学生的认知接受范围。那么,小学生又该怎么思考呢?
那就是数形结合地进行分析,再等积变形,重新构造新的图形,于是算法算理就一目了然了(如下图)。
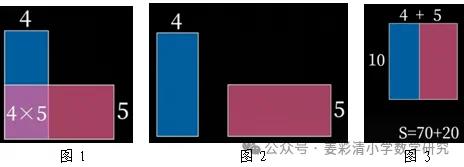
由图上的数据可知,蓝色长方形与红色长方形的重叠部分为4×5=20平方厘米,所以将这这两个长方形拿开,重新拼成图3那样,则新的长方形面积为70+20=90平方厘米,它的一条边为4+5=9厘米,所以原来正方形的边长为90÷9=10厘米,因此原来正方形的面积为10×10=100平方厘米。

综上所述,数学思维不同于一般性思维,它最大的“魅力”在于它具有严密性与精准性,以及妙用符号化的简化表达方式,更让人沉醉其中的是,我们在数学分析与推理的基础上,创造性进行数量关系再“构造”,从而转化出“新的图形”或“新的情境”,让数量关系明朗起来,因而难题也就不难了。
时间不早了,今天就说这么多了。下次有时间,我再举一些例子,让大家更好地了解数学思维的特点,从而更好地学好数学这门学科!
